A pen and paper exercise around Plato’s Timaeus suggest a brief discussion regarding:

• The number of triangles required to construct each elemental solid, and
• The omission of certain other polyhedra as elemental structures

may be useful, or at the very least highlight some oversight or misconceptions on my part.

Elemental Triangles

Depth, moreover, is of necessity comprehended within surface, and any surface bounded by straight lines is composed of triangles. Every triangle, more-over, derives from two triangles, each of which has one right angle and two acute angles. Of these two triangles, one [the isosceles right-angled triangle] has at each of the other two vertices an equal part of a right angle, determined by its division by equal sides; while the other [the scalene right-angled triangle] has unequal parts of a right angle at its other two vertices, determined by the division of the right angle by unequal sides.

Of the many [scalene right-angled] triangles, then, we posit as the one most excellent, surpassing the others, that one from [a pair of] which the equilateral triangle is constructed as a third figure.

Timaeus goes on to state that the scalene is the building block of fire, air, and water, whilst the isosceles is that of Earth. Following Timaeus description of the elemental scalene, and specifically the requirement to form an equilateral triangle from a pair of scalenes I believe the triangle to which he refers to be this:

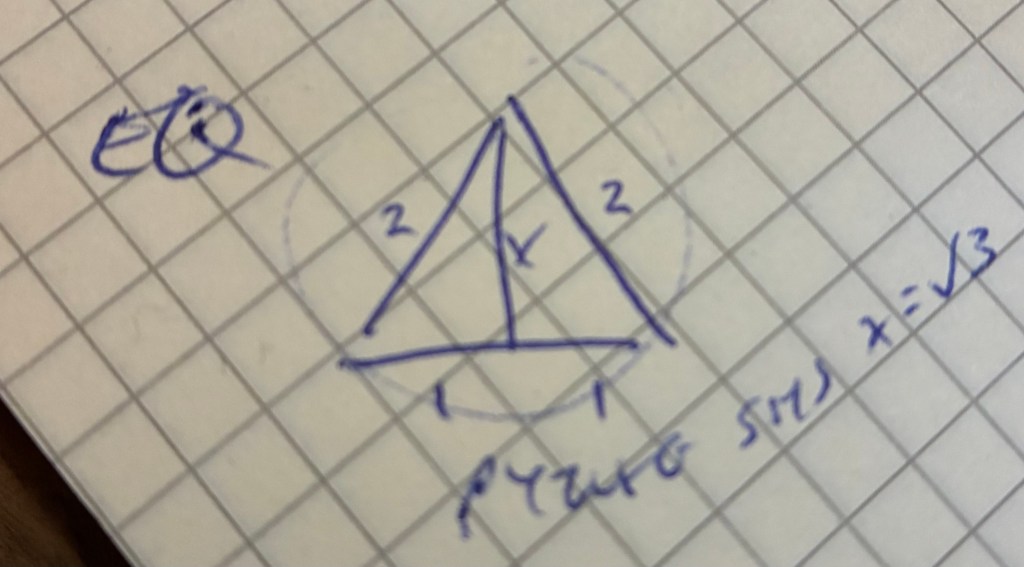
Here two scalenes with side lengths as shown, placed ‘back to back’ produce an equilateral triangle of side length two.

Timaeus describes the structure of Fire as:

Leading the way will be the primary form [the tetrahedron], the tiniest structure, whose elementary triangle is the one whose hypotenuse is twice the length of its shorter side.

So far, so good. Our hypotenuse is indeed twice the length of the shorter side and we know that a regular tetrahedron has four equilateral triangle faces.

Now when a pair of such triangles are juxtaposed along the diagonal [i.e., their hypotenuses] and this is done three times, and their diagonals and short sides converge upon a single point as center, the result is a single equilateral triangle, composed of six such triangles.

This sentence can be read in a number of ways. The previous diagram does not help as its back to back scalene arrangement has already produced an equilateral triangle using just those two scalenes. If we ignore that equilateral and constrain ourselves to Timaeus requirements the following arrangement is arrived at. The shaded section shows the initial juxtaposition along the hypotenuse, which is done three times, and finally arranged such that the junction of each shorter side and the hypotenuse is central:

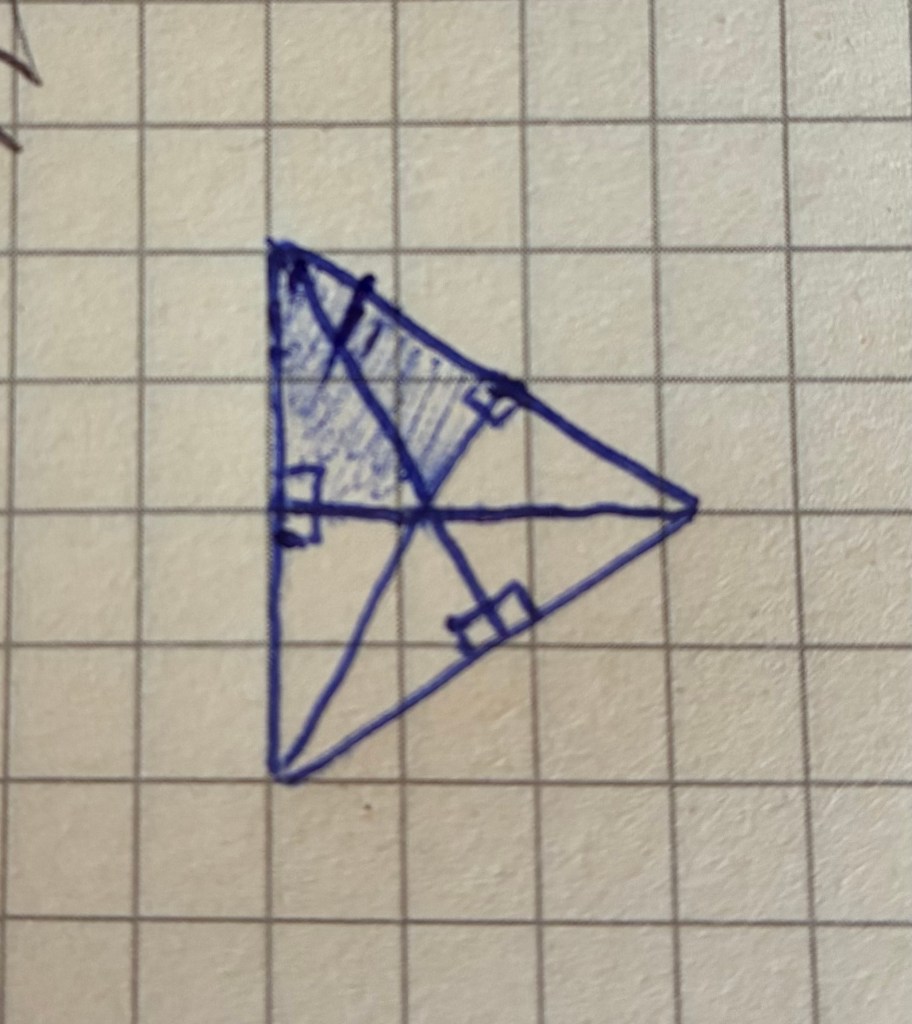
When four of these equilateral triangles are combined, a single solid angle is produced at the junction of three plane angles. This, it turns out, is the angle which comes right after the most obtuse of the plane angles. And once four such solid angles have been completed, we get the primary solid form, which is one that divides the entire circumference [sc. of the sphere in which it is inscribed] into equal and similar parts.

The rest is straightforward. We can lay out a pattern of four of the above equilaterals in several ways which when cut out and folded will produce the four equilateral triangle faces of a regular tetrahedron.

The possible readings in this construction and the omission of the total number of scalenes required to construct the tetrahedron in this manner mean that it is worth stating that Timaeus’ method requires four equilaterals, each of which is comprised of six scalenes. Thus a total of twenty-four scalenes are required, not the eight that the back-to-back equilateral from a scalene pair would require.

The second element, air, is a regular octahedron and as such, using the six scalene equilateral building block as above requires eight equilaterals, each of which is comprised of six scalenes. This a total of forty-eight scalenes are required. Timaeus is keen to show that the elemental scalene can be assembled and disassembled repeatedly, for example here where the forty-eight scalenes required for a unit element of air could be sourced from two deconstructed unit elements of fire.

At the risk of stating the obvious the fire tetrahedron is by definition a triangular based pyramid. Timaeus air octahedron by contrast is a bi-pyramidal square based pyramid (note the square base does not form part of the solid’s faces construction, being wholly internal to the solid, and therefore requires no scalene or otherwise triangles for its construction).

Timaeus’ third element, water, is the last element derived from the elemental scalene. Its surface faces are comprised of equilaterals arranged such that the bases of any five that share a common vertex form a pentagon in the base plane. We know this structure as a regular icosahedron.

Now the third body [the icosahedron] is made up of a combination of one hundred and twenty of the elementary triangles, and of twelve solid angles, each enclosed by five plane equilateral triangles. This body turns out to have twenty equilateral triangular faces.

Given Timaeus does not state the number of elementary (scalene) triangles for fire and air the statement that the icosahedron requires one hundred and twenty of them may seem at odds to the forty that use of the simple equilateral comprised of two back to back scalenes would suggest. However, using equilaterals comprised of six scalenes does indeed mean that one hundred and twenty are required to cover the solid’s surface. Thus a unit element of water could be comprised of deconstructed scalenes from three unit elements of fire and one unit element of air, or any other combination.

It is at this point that Timaeus dispenses with the scalene triangle and introduces the 90-45-45 isosceles triangle, leading to this statement:

While there are indeed four kinds of bodies that come to be from the [right-angled] triangles we have selected, three of them come from triangles that have unequal sides, whereas the fourth alone is fashioned out of isosceles triangles. Thus not all of them have the capacity of breaking up and turning into one another, with a large number of small bodies turning into a small number of large ones and vice-versa. There are three that can do this. For all three are made up of a single type of triangle, so that when once the larger bodies are broken up, the same triangles can go to make up a large number of small bodies, assuming shapes appropriate to them. And likewise, when numerous small bodies are fragmented into their triangles, these triangles may well combine to make up some single massive body belonging to another kind.

The fact that square faces of the cube are derived from a pair of 90-45-45 isosceles juxtaposed along their hypotenuse again raises the question of why a pair of scalenes back to back was not sufficient as the building block of the equilateral triangle based elements.

Other Polyhedra

Timaeus describes five elemental structures in total, the three we have covered (fire, air, and water), the isosceles derived cube (earth), and a fifth:

One other construction, a fifth, still remained, and this one the god used for the whole universe, embroidering figures on it.

Given that small set of elemental structures (four defined and one undefined) one may wonder why other polyhedra are omitted.

The simplest example of a ‘skipped’ polyhedron can be seen between Timaeus’ fire tetrahedron (triangular based pyramid) and air octahedron (bi-pyramidal square based pyramid). Using Timaeus standard six scalene equilateral we might ask, “Where is the bi-pyramidal triangular based pyramid?”

This would have six equilateral triangular sides and thus require thirty-six elemental scalenes in total. In the absence of a diagram think of two fire tetrahedrons stuck together by one of any of their respective four faces, but as with the square based pyramids comprising the octahedron we remove the triangular bases as they are internal).

Similarly we might expect between air (octahedron) and water (icosahedron) a sequence of bi-pyramidal structures, for example a pentagon based one having ten equilateral triangle faces. Extending the sequence further is problematic of course – six equilateral triangles sharing a common central point will ‘flatten’ into a simple two dimensional hexagon without the need for an ‘uplift’ in the centre to bring the base sides together. The bi-pyramidal sequence has thus reached its natural conclusion of collapsing a dimension of space.

If we now return to the selection of tetrahedron, octahedron, but not the bi-pyramidal pentagonal based pyramid the unspoken requirement for an elemental solid presents itself – all of its vertices must be identical. The bi-pyramidal pentagonal based pyramid has distinct flattening around the ‘waist’ giving it two different groups of similar vertices. Since the tetrahedron is not bi-pyramidal we can say that the octahedron is the only bi-pyramidal pyramid the elemental selection criteria.

Spherical Packing

With those two discussions neatly concluded (pending feedback highlighting errors on my part), one might have wondered about polyhedron ‘size’ along the way or rather how uniform inter-vertex distance emerges. Having sought without success in the dog’s toys (for tennis balls) and the kitchen (for oranges) the following thoughts on spherical packing in relation to elemental structure are purely conjecture.

Were we to have access to physical spheres to experiment with we might start by arranging our spheres on the floor (two dimensions). For example four spheres may be tightly grouped on the floor into a two by two arrangement, the sphere’s centres forming a perfect square. However, we could also place three of the spheres such that their centres formed an equilateral triangle parallel to the plane of the floor, and then place the fourth in the dip created at the centre point of the triangle of spheres.

I do not have the wherewithal to verify that a two by two arrangement consumes more three dimensional space than the tetrahedral arrangement in the second example but my sense it that it must. Perhaps then the tetrahedron that is Timaeus’ fire is the ‘tightest’ arrangement of four spheres in three dimensional space.

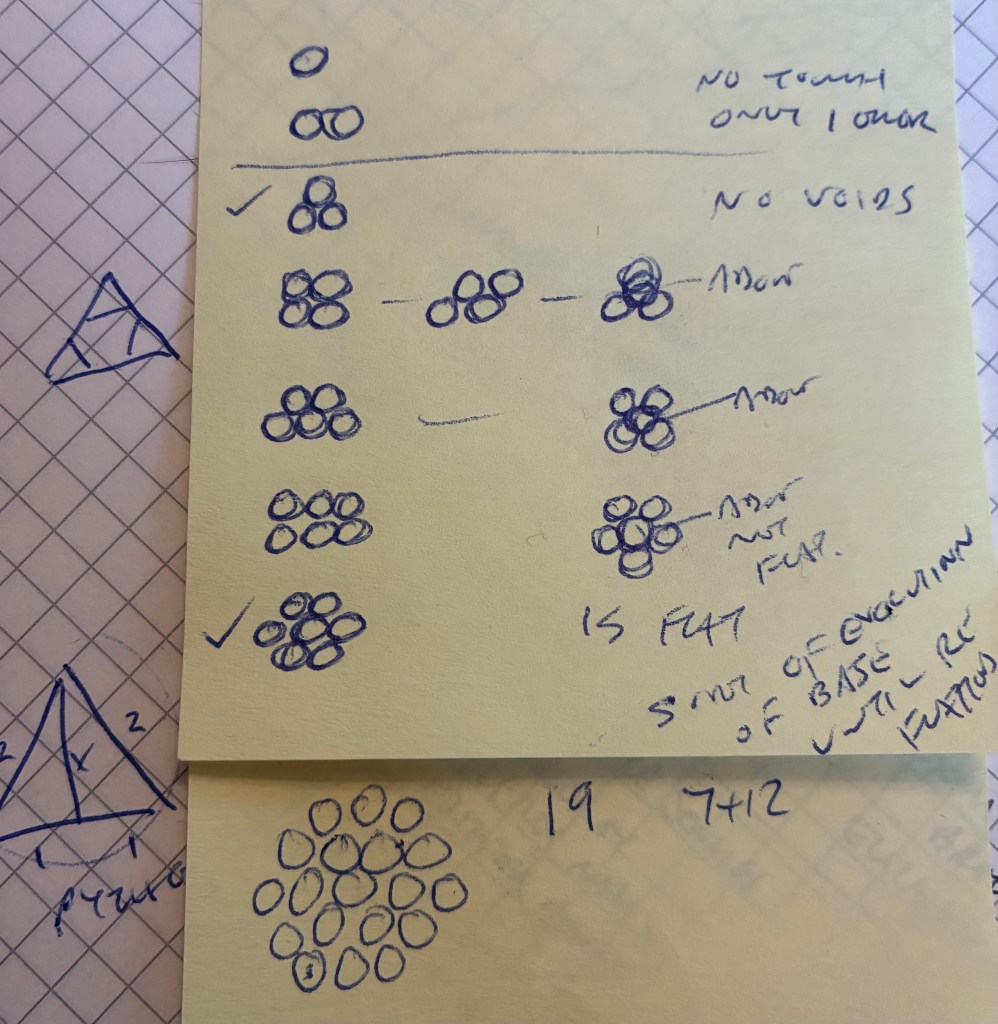
With five spheres we might arrange them in a two by two base with the last in the central dip, creating a square based pyramid (would such a pyramid have equilateral triangle sides?), and again my sense is that this must be ‘tighter’ than than a two dimensional arrangement (especially if we notice that we have four sides worth of the tightest arrangement of three spheres).

The fifth sphere and our previous work with four gives us a third option though. If we lift our tetrahedral arrangement of four spheres and place the fifth sphere in the central dip underneath (opposite the one we placed in the dip on top) we would have a bi-pyramidal triangular based pyramid mentioned in the previous section.

Similarly with six spheres in hand, the sixth might be better placed in the lower dip of our five sphere square based pyramid and in fact such an arrangement would produce a perfect octahedron (Timaeus’ air). Another experimenter thinking outside the box might arrange their spheres connected at angles through each other of one hundred and twenty degrees, creating a two dimensional hexagon (indeed they may have created a pentagon of spheres at offsets of one hundred and eight degrees in the previous step with their five spheres).

Seven spheres gives a double tip pentagonal arrangement option creating a bi-pyramidal pentagon based pyramid, and the unprecedented option of, back in two dimensions, placing the seventh sphere into the hole left in the two dimensional hexagon of the previous step. Like the discussion of the hexagonal based polyhedron, no ‘uplift’ is required to accommodate our seventh sphere such an operation has become redundant.

At the risk of descending into spherical madness and in order to draw a conclusion, let us beg our sphere handler for just one more sphere (for a total of eight) and go back to basics with a two vertical layer, two by two plane of spheres. The resultant sphere centres mark the corners of a perfect cube, ie Timaeus’ Earth elemnt. The lack of ‘dip’ use to construct this cube perhaps corresponds to the shift Timaeus had to make away from scalenes by introducing the isosceles, but the fact that we are still only working with uniform spheres might have made Timaeus wonder about Earth’s immutability to/from other elements.